Fermat 점 (페르마 점)은 Euclid 평면 (유클리드 평면) \(\mathbb E\)에서 주어진 세 점이 있을 때, 그 세 점들까지의 거리의 합이 최소인 점을 말한다. 본 포스트에서는
Fermat 점에서 세 꼭짓점까지 이루는 직선들은 서로 120도를 이룬다
는 명제를 조건부 극값 문제를 해결하는 해석적인 증명과 평면 기하적인 증명, 두 가지로 보인다.
해석적인 증명
본 증명은 Lagrange 승수법을 통해 조건부 극값 문제를 해결하여 주어진 명제를 증명한다. 가장 단순하면서도 계산이 복잡한 방식이다.
삼각형 \(\mathrm{ABC}\)와 그 내부의 점 \(\mathrm K\)를 잡자. 이 때,
\[\mathrm{AB} = c, \mathrm{BC} = a, \mathrm{CA} = b,\\ \mathrm{AP} = x, \mathrm{BP} = y, \mathrm{CP} = z,\\ \angle \mathrm{APB} = \gamma = 2\pi - \alpha - \beta, \angle \mathrm{BPC} = \alpha, \angle \mathrm{CPA} = \beta\]으로 설정하고, 함수 \(f: \mathbb{E} \rightarrow \mathbb{R}\)는 \(f(P) = x + y + z\)로 정의하자. Fermat 점을 찾는 문제가 \(f\)의 극값을 구하는 문제로 바뀌었다. 단, 주어진 세 점 \(\mathrm{A, B, C}\)는 삼각형을 이루므로 다음의 세 조건을 만족한다.
\[x^2 + y^2 - 2xy \cos (2\pi - \alpha - \beta) = c^2,\\ y^2 + z^2 - 2yz \cos \alpha = a^2,\\ z^2 + x^2 - 2zx \cos \beta = b^2\]이제 다음과 같이 \(\mathbb E\)에서 \(\mathbb R\)로 가는 세 함수를 정의할 수 있다:
\[g_1 (P) = x^2 + y^2 - 2xy \cos (\alpha + \beta) - c^2,\\ g_2 (P) = y^2 + z^2 - 2yz \cos \alpha - a^2,\\ g_3 (P) = z^2 + x^2 - 2zx \cos \beta - b^2\]Lagrange 승수법을 사용하기 위해 다음과 같은 새로운 함수 \(\tilde f: \mathbb{E} \rightarrow \mathbb{R}\)를 정의하자:
\[\tilde f(P) = f(P) - \sum_{i = 1}^3 \lambda_i g_i (P)\]이제 좀 골치 아픈 작업이 남았다—\(\tilde f\)의 극값을 구하기 위해 \(x, y, z, \alpha, \beta\)에 대해서 식을 편미분하자.
\[(1)\ \frac{\partial \tilde f}{\partial x} = 1 - 2 \lambda_1 x + 2 \lambda_1 y \cos (\alpha + \beta) - 2 \lambda_3 x + 2 \lambda_3 z \cos \beta = 0\\ (2)\ \frac{\partial \tilde f}{\partial y} = 1 - 2 \lambda_1 y + 2 \lambda_1 x \cos (\alpha + \beta) - 2 \lambda_2 y + 2 \lambda_2 z \cos \alpha = 0\\ (3)\ \frac{\partial \tilde f}{\partial z} = 1 - 2 \lambda_2 z + 2 \lambda_2 y \cos \alpha - 2 \lambda_3 z + 2 \lambda_3 x \cos \beta = 0\\ (4)\ \frac{\partial \tilde f}{\partial \alpha} = 2 \lambda_1 xy \sin (\alpha + \beta) + 2 \lambda_2 yz \sin \alpha = 0\\ (5)\ \frac{\partial \tilde f}{\partial \beta} = 2 \lambda_1 xy \sin (\alpha + \beta) + 2 \lambda_3 zx \sin \beta = 0\]항 하나가 완전히 일치하는 (4)와 (5)를 연립하면 \(\frac{\lambda_2 \sin \alpha}{\lambda_3 \sin \beta} = \frac x y\)이 된다. 이 때 \(x = k \lambda_2 \sin \alpha\)라고 두고 다시 (4)나 (5)에 대입하면, \(x, y, z\) 모두 \(k, \alpha, \beta\)만으로 표현할 수 있게 된다.
\[x = k \lambda_2 \sin \alpha,\\ y = k \lambda_3 \sin \beta,\\ z = k \lambda_1 \sin (\alpha _ \beta)\]이렇게 다시 쓴 \(x, y, z\)를 (1)–(3)에 대입하여 식을 정리하고 \(\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\)를 대입하면,
\[\sin \alpha = X,\\ \sin \beta = X,\\ \sin (\alpha + \beta) = X\]가 나온다. 이 때, \(X\)는 식을 정리하면서 나온 어떤 값이다. 결국 \(\alpha = \beta = 120^\circ\)를 알 수 있다.
그런데, 이 증명에는 흠이 있는데, Lagrange 승수법의 한계상, 이미 \(f\)는 극값을 가진다는 것이 전제된다. 즉, 필요 조건일 뿐이지 충분 조건이 되지 않는다. 예컨데 삼각형의 한 내각이 120돌르 넘는다면, Fermat 점에서 각 꼭짓점들을 이은 직선들은 서로 이루는 각이 120도가 될 수 없다.
이에 우리는 이 문제를 해결할 수 있는 기하적인 증명을 제시한다.
기하적인 증명
삼각형 \(\mathrm{ABC}\)와 그 내부의 한 점 \(F'\)를 잡자.
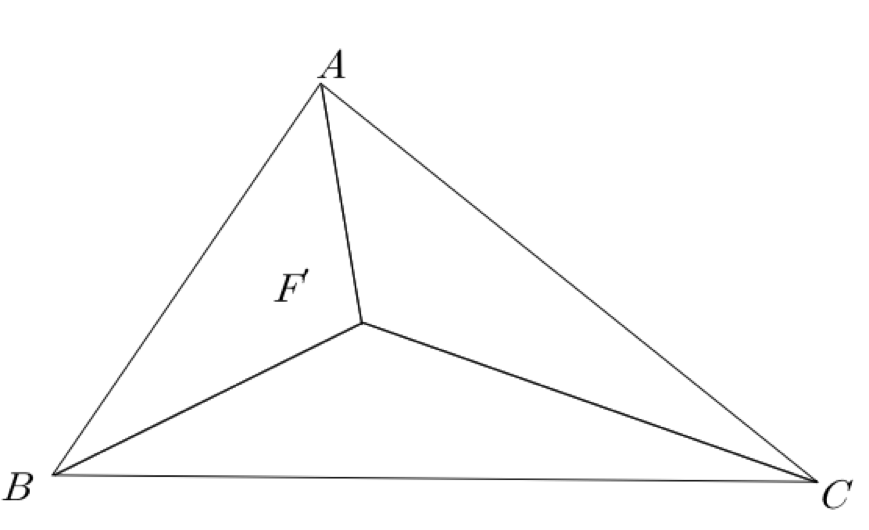
이 \(\triangle \mathrm{ABC}\)를 점 \(\mathrm B\)에 대해 반시계 방향으로 60도 회전한다. 이렇게 회전된 삼각형과 점을 각각 \(\triangle \mathrm{A'BC}, F''\)으로 두자.
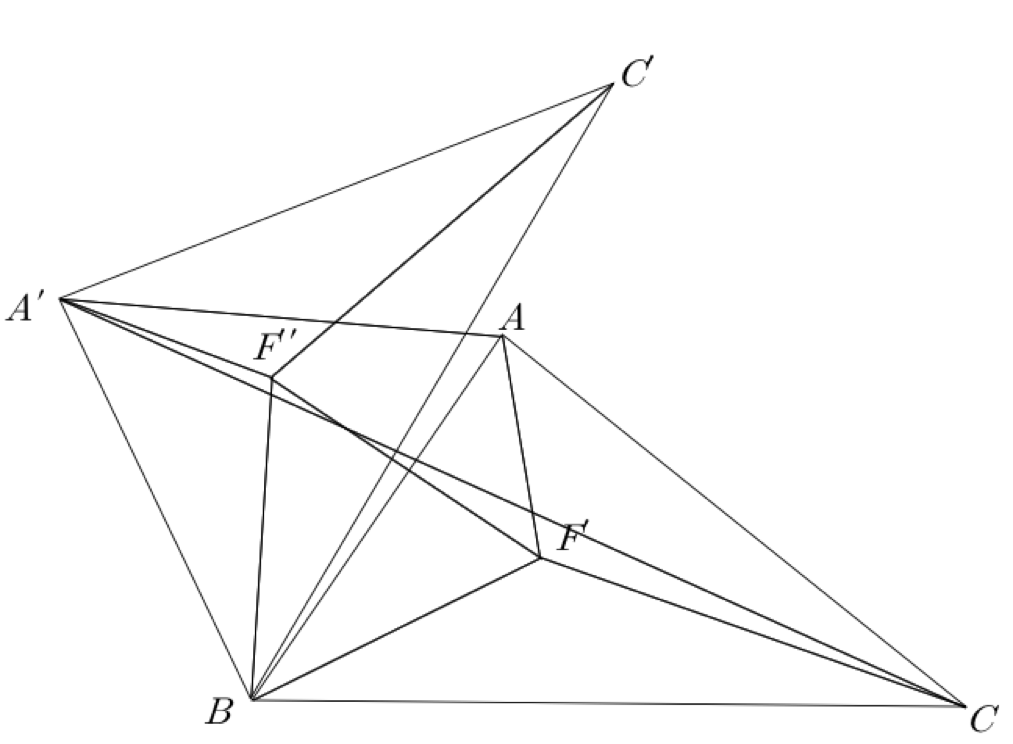
그렇다면 \(\mathrm{AF' + BF' + CF' = A'F'' + F''F' + F'C}\)이며, 이의 최솟값은 \(\mathrm{A'C}\)가 된다. (Euclid 평면에서 최단거리는 직선이기 때문이다.) \(\mathrm{A'B = BA = AA'}\)이므로 \(\triangle \mathrm{AA'B}\)는 정삼각형이다. 즉, \(\mathrm A'\)은 \(\triangle \mathrm{ABC}\) 외부에 \(\mathrm{AB}\)와 정삼각형을 이루도록 잡은 점이다.
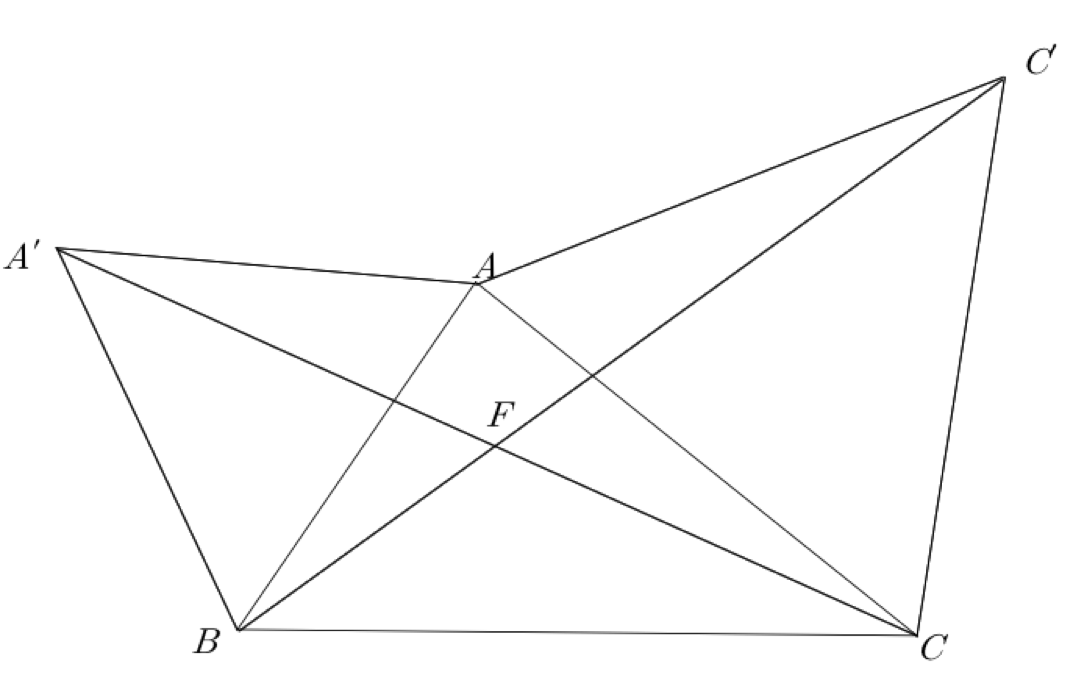
마찬가지로, \(\triangle \mathrm{BB'C}\)가 정삼각형이 되도록 \(\mathrm B'\)을 \(\triangle \mathrm{ABC}\) 밖에 잡을 수 있다. 따라서 \(\mathrm{AF' + BF' + CF'}\)이 최소인 \(\mathrm F'\)은 \(\mathrm{CA'}\)과 \(\mathrm{AB'}\)의 교점에 위치할 때이며, 이를 \(\mathrm F\)라고 하자.
또한, \(\mathrm{A'A = BA, \angle A'AC = \angle BAC', AC = AC'}\)이므로 \(\triangle \mathrm{A'AC} \equiv \triangle \mathrm{BAC}\ (SAS)\)이다. 결국 \(\angle \mathrm{ABF} = \angle \mathrm{AA'F}\)이어서 \(\mathrm{A, A', B, F}\)는 concyclic, 즉 한 원 위에 있다. 따라서 \(\mathrm{\angle AFB = 180^\circ - \angle AA'B = 120^\circ}\)이다.
그런데, 위 증명에서는 삼각형의 내각이 모두 120도 이하일 경우만을 고려한 것이다. 왜인지 알겠는가? \(\mathrm{A, A', B, F}\)가 한 원 위에 있다고 하였을 때, \(\angle \mathrm{BAC}\)가 120도를 넘었더라면 네 점의 외접원 내부에 \(\mathrm A\)가 들어와 문제가 되기 때문이다. 이런 경우를 따로 고려해줘야한다.
간단히 개요만 설명한다. \(\angle \mathrm{BAC}\)가 120도를 넘는다고 하자. 그렇다면 삼각형 내부의 어떤 점이든 각 꼭짓점까지의 거리 합이 \(\mathrm{AB + AC}\)보다 작은 점이 없다는 것은 위 증명을 조금 변형하여 알 수 있다. 이제 아래와 같은 lemma를 설정하자.
삼각형 외부의 어떤 점이든, 각 꼭짓점까지의 거리 합은 그 삼각형 둘레에 존재하는 점에서 각 꼭짓점까지의 거리의 합보다 작다.
삼각형의 각 변을 직선으로 연장하여 평면을 총 6구역으로 나눌 수 있는데, 각 구역에 존재하는 점에서 각 꼭짓점까지의 거리 합보다 작은 삼각형 둘레 상의 점을 쉽게 찾을 수 있다. 일반성을 잃지 않고 삼각형의 꼭짓점이 그 무한 영역의 끝이 아닌 경우와 삼각형의 변이 무한 영역의 경계인 경우 두 구역에 대해서만 확인해보면 된다. 이렇게 lemma를 증명하면, \(\mathrm A\)가 Fermat 점이 됨을 알 수 있다.